【Python】線形探索【アルゴリズム】
Pythonでアルゴリズムの線形探索の解説をします。
線形探索とは
要素が直線状に並んだ配列からの探索は、目的とする値(キー)を持つ要素を先頭から順番に調べることで見つかります。
この探索法を線形探索(linear search)または逐次探索(sequential search)といいます。
この線形探索を具体的な例で説明します。
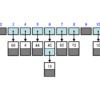
まずは配列4、1、5、3、6、3、7から3を探索します。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
表中の青色の数字が探索中のインデックス(添え字)で赤色の数字が対応するキー(値)です。
探索の様子は以下の通りです。
①添え字0の要素4に注目する。目的の値ではない。
②添え字1の要素1に注目する。目的の値ではない。
③添え字2の要素5に注目する。目的の値ではない。
④添え字3の要素3に注目する。目的の値であるため探索に成功。
①から④まで先頭から1つずつ要素を調べていき、目的とする値(キー)が見つかった(探索成功)時点で探索は終了します。
この配列では3は添え字5にもありますが、より先頭側の3で見つかるため後の要素の探索は行われません。
今度は同じ配列で2を探索します。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 5 | 3 | 6 | 3 | 7 |
配列の要素を先頭から順番に調べますが、キーと同じ値を持つ要素を見つけることは最後までありません。
キーが最後まで見つからなかった場合、キーと同じ値を持つ要素が配列内に存在しないため探索失敗となります。
この成功例と失敗例から線形探索の終了条件は2つあることがわかります。
探索失敗:探索する値が見つからず終端を通り越しそうになった。
探索成功:探索する値と等しい値を見つけた。
これらの条件をプログラムで書くことを考えます。
探索する配列をa、表内の青字に相当する注目している添え字をカウンタ変数iとします。
iの初期値を0として要素を1つ探索するごとに1ずつインクリメントしていきます。
目的とする値をkeyとしたとき終了条件は以下のように表されます。
探索失敗:i == len(a)が成立
探索成功:a[i] == keyが成立
これらを抑えたうえで線形探索のプログラムは以下のようになります。
線形探索のソースコード
コード例
# 線形探索(while文)
from typing import Any, Sequence
def linear_search(a: Sequence, key: Any) -> int:
"""シーケンスaからkeyと等価な要素の線形探索(while文)"""
i = 0
while True:
if i == len(a):
return -1 # 探索失敗(-1を返却)
if a[i] == key:
return i # 探索成功(添え字を返却)
i += 1
if __name__ == '__main__':
num = int(input('要素数 : '))
x = [None] * num # 要素数numの配列を生成
for i in range(num):
x[i] = int(input(f'x[{i}] : '))
search_key = int(input('探す値 : ')) # キーsearch_keyの読み込み
idx = linear_search(x, search_key) # xからsearch_keyと等価な要素を探索
if idx == -1:
print('その値の要素は存在しません。')
else:
print(f'{search_key}はx[{idx}]にあります。')実行結果(探索成功)
要素数 : 7
x[0] : 4
x[1] : 1
x[2] : 5
x[3] : 3
x[4] : 6
x[5] : 3
x[6] : 7
探す値 : 3
3はx[3]にあります。実行結果(探索失敗)
要素数 : 7
x[0] : 4
x[1] : 1
x[2] : 5
x[3] : 3
x[4] : 6
x[5] : 3
x[6] : 7
探す値 : 2
その値の要素は存在しません。関数linear_searchは配列aから値がkeyの要素を線形探索します。
numには配列の要素数、xには配列の要素の値、search_keyには探す値をinput関数で入力させます。
関数linear_search内ではカウンタ用変数iを0で初期化します。
while文ではa[i]の値を先頭から順番に調べていきます。
その際に調べた後に次の要素に移動するためiを1ずつインクリメントします。
探索していく最中でkeyと同じ値であればそのときのiの値を返却します。
配列の最後の要素を調べてkeyと同じ値が見つからなかったときは-1を返すようにします。
idxには関数linear_searchによって返却されたiの値または-1が格納されます。
最後のif文ではその値に応じて表示する内容を分岐しています。
なお関数linear_searchはfor文で書き換えると短く簡潔になります。
def linear_search(a: Sequence, key: Any) -> int:
"""シーケンスaからkeyと等価な要素の線形探索(for文)"""
for i in range(len(a)):
if a[i] == key:
return i # 探索成功
return -1 # 探索失敗他の部分はまったく同じなので関数linear_searchの箇所だけ掲載しています。
関数linear_searchはアノテーションより任意のシーケンスからの探索が行えるようになっています。
そこでint型以外の要素を持つリストやタプル、文字列に対しても線形探索ができます。
コード例
# 線形探索を行う関数linear_searchの利用例
from linear_search_while import linear_search
t = (2, 4.5, 3.14, 7, 5.9, 6)
s = 'universe'
a = ['AAA', 'BBB', 'CCC']
print(f'{t}中に3.14は添え字{linear_search(t, 3.14)}にあります。')
print(f'{s}中に"v"は添え字{linear_search(s, "v")}にあります。')
print(f'{a}中に"AAA"は添え字{linear_search(a, "AAA")}にあります。')実行結果
(2, 4.5, 3.14, 7, 5.9, 6)中に3.14は添え字2にあります。
universe中に"v"は添え字3にあります。
['AAA', 'BBB', 'CCC']中に"AAA"は添え字0にあります。準備として前の線形探索(while文)のプログラムをlinear_search_while.pyとして保存します。
そのプログラムを保存したフォルダに今回のプログラムを保存するようにします。
配列tはint型とfloat型の混在のタプル、sはstr型の文字列、aはstr型の文字列のリストです。
int型もfloat型もstr型もシーケンスなので線形探索が正しく適応できます。
線形探索は単純でわかりやすく要素がランダムに並んでいても探索が行えますが、終了条件が2個あるので効率はあまりよくないです。
この終了条件を1個に減らしてさらに効率よく探索を行えるのが番兵法です。