【Python】2分探索【アルゴリズム】
Pythonでアルゴリズムの2分探索の解説をします。
2分探索とは
2分探索(binary search)は要素がキーの昇順・降順にソートされて並んだ配列からの探索を行うアルゴリズムです。
今回は昇順に並んだ配列aからの2分探索を考えます。
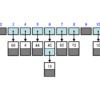
配列aには4、6、12、23、29、32、43、51、70、76、84が格納されているとします。
この配列から43を探索します。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 |
まず配列の中央に位置するa[5]の値32に着目します。
値32は探している値43よりも小さい値です。
昇順になっているのでこの配列は先頭にいくほど小さい値で、末尾に行くほど大きい値になります。
つまり探している値43はa[5]より後ろの要素であるa[6]からa[10]にある可能性があります。
そこで探索範囲をa[6]からa[10]に絞り込みます。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 |
絞り込んだ範囲の中央に位置するa[8]の値70に着目します。
値70は探している値43よりも大きい値です。
探している値43はa[8]より先頭の要素であるa[6]からa[7]にある可能性があります。
このときすでに探索範囲から除外にしたa[0]からa[5]は含まれません(もうないのがわかっているから)。
そこで探索範囲をa[6]からa[7]に絞り込みます。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 |
絞り込んだ範囲の中央に位置するa[6]の値43に着目します。
中央要素の添え字は二つの添え字の中央値(6 + 7) // 2 = 6から求めています。
着目している値43は探している値(キー)なので探索成功です。
2分探索(探索成功)
n個の要素が昇順に並んだ配列aからキーkeyを2分探索するプログラムを考えます。
探索範囲の先頭、末尾、中央の添え字をそれぞれpl、pr、pcとします。
探索開始時点でのplは0、prはn – 1、pcは(n – 1) // 2と表されます。
| Ⅰ | pl | pc | pr | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅱ | pl | pc | pr | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅲ | pl pc |
pr | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 |
探索範囲は表内の背景が白の要素で、背景が灰色の要素は探索対象から除外された範囲です。
Ⅲのようにa[pc]とkeyを比較して等しければ探索成功です。
一致しない場合は次の2つのように探索範囲を絞ります。
a[pc] < keyのとき(ⅠからⅡ)
a[pl]からa[pc]はkeyよりも小さい値であるのがわかるので探索対象から外します。
探索範囲はa[pc + 1]からa[pr]に絞り込めます。
そのためplの値をpc + 1に変更します。
a[pc] > keyのとき(ⅡからⅢ)
a[pc]からa[pr]はkeyよりも大きい値であるのがわかるので探索対象から外します。
探索範囲はa[pl]からa[pc – 1]に絞り込めます。
そのためprの値をpc – 1に変更します。
よって探索範囲の絞り込み方は以下のようになります。
| 中央値 a[pc]が keyより 小さい |
左端plを中央の一つ右に移動して 探索範囲を後半に絞り込む |
|---|---|
| 中央値 a[pc]が keyより 大きい |
右端prを中央の一つ左に移動して 探索範囲を前半に絞り込む |
2分探索(探索失敗)
次に2分探索で失敗する例を考えます。
同じ配列aから5を探索します。
| Ⅰ | pl | pc | pr | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅱ | pl | pc | pr | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅲ | pl pc |
pr | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅳ | pl pr pc |
||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 | |
| Ⅴ | pr | pl | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 6 | 12 | 23 | 29 | 32 | 43 | 51 | 70 | 76 | 84 |
Ⅰでは探索範囲を配列全体のa[0]からa[10]としています。
中央要素のa[5]の値32はkeyの値5より大きいです。
prをa[5]の直前のa[4]として探索対象をa[0]からa[4]に絞ります。
Ⅱでは探索範囲をa[0]からa[4]としています。
中央要素のa[2]の値12はkeyの値5より大きいです。
prをa[2]の直前のa[1]として探索対象をa[0]からa[1]に絞ります。
Ⅲでは探索範囲をa[0]からa[1]としています。
中央要素のa[0]の値4はkeyの値5より小さいです。
plをa[0]の直後のa[1]とすることでplとprは1となり、探索対象をa[1]に絞ります。
Ⅳでは探索範囲をa[1]としています。
中央要素のa[1]の値6はkeyの値5より大きいです。
prをa[1]の直前のa[0]としますが、Ⅴのようにplがprよりも大きくなってしまい探索範囲がなくなります。
これにより探索失敗となります。
成功例と失敗例により2分探索の終了条件は次の2つがあることがわかります。
| 終了条件 | 式 |
|---|---|
| ①a[pc]とkeyが 一致 |
a[pc] == key |
| ②探索範囲が なくなる |
pl > pr |
以上により2分探索のプログラムは以下のようになります。
2分探索のソースコード
コード例
# 2分探索
from typing import Any, Sequence
def binary_search(a: Sequence, key: Any) -> int:
"""シーケンスaからkeyと一致する要素を2分探索"""
pl = 0 # 探索範囲先頭の添え字
pr = len(a) - 1 # 探索範囲末尾の添え字
while True:
pc = (pl + pr) // 2 # 中央要素の添え字
if a[pc] == key:
return pc # 探索成功
elif a[pc] < key:
pl = pc + 1 # 探索範囲を後半に絞る
else:
pr = pc - 1 # 探索範囲を前半に絞る
if pl > pr:
break
return -1 # 探索失敗
if __name__ == '__main__':
num = int(input('要素数 : '))
x = [None] * num # 要素数numの配列を生成
print('注意 : 昇順に入力すること。')
x[0] = int(input('x[0] : '))
for i in range(1, num):
while True:
x[i] = int(input(f'x[{i}] : '))
if x[i] >= x[i - 1]:
break
search_key = int(input('探す値 : ')) # キーsearch_keyの読み込み
idx = binary_search(x, search_key) # xからsearch_keyと等価な値を探索
if idx == -1:
print('その値の要素は存在しません。')
else:
print(f'{search_key}はx[{idx}]にあります。')実行結果(探索成功)
要素数 : 7
注意 : 昇順に入力すること。
x[0] : 12
x[1] : 23
x[2] : 29
x[3] : 32
x[4] : 43
x[5] : 51
x[6] : 70
探す値 : 29
29はx[2]にあります。実行結果(探索失敗)
要素数 : 7
注意 : 昇順に入力すること。
x[0] : 12
x[1] : 23
x[2] : 29
x[3] : 32
x[4] : 43
x[5] : 51
x[6] : 70
探す値 : 40
その値の要素は存在しません。2分探索では探索対象の配列が昇順または降順にソートされている必要があります。
プログラムではひとつ前に入力された値よりも小さい値が入力された場合は再入力させるようにしています。
なお最初の要素の入力は再入力させる必要がないのでwhileループ文の外にしています。